Ringkasan Materi Gerak Melingkar Beraturan (GMB) Beserta Contohnya

Contoh soal fisika kelas 10 soal fisika kelas 10 semester 2 soal fisika kelas 10 semester 2 dan pembahasannya latihan soal fisika kelas 10 contoh soal fisika kelas 9 soal fisika kelas 8 semester 2 Latihan soal Fisika kumpulan soal fisika kelas 10 latihan soal fisika kelas 10 semester 2 kumpulan soal fisika smp dan pembahasannya kumpulan soal fisika kelas 11 soal fisika kelas 7 semester 1 latihan soal fisika kelas 12 semester 1 download soal fisika kelas 11.

Ringkasan Materi Gerak Melingkar Beraturan (GMB) Beserta Contohnya - Gerak melingkar merukan salah satu contoh gerak dua dimensi yang lintasanya melingkar. Mengapa sebuah benda dapat bergerak mengkar?. Nah, hal ini dikarenakan ada sebuah gaya yang selalu membelokkan benda tersebut yang arah gaya tersebut selalu menuju ke arah pusat lingkaran. Gaya ini disebut sebagai gaya sentripetal, yaitu sebuah gaya yang arahnya menuju pusat lingkaran.

Jika anda mengikat sebuah benda (misalkab bola beker) pada salah satu ujung tali kemudian ujung tali lainya anda putar maka benda tersebut akan bergerak melingkar. Kenapa benda tersebut dapat bergerak secara melingkar dan tidak terpental jauh. Hal ini dikarenakan tali menahan bola tersebut sehingga tidak keluar dari lintasan melingkar. Pada tali bekerja sebuah gaya tetangan tali yang merupakan gaya sentripetal dari sistem tersebut. Jarak antara benda dengan tangan (pusat lintasan lingkaran) adalah sama dengan jari-jari lintasan lingkaran yang dibentuk oleh benda.

Baca Juga : Contoh Soal dan Jawaban Hukum 2 Newton Serta Konsepnya

Apa buktinya bahwa tali tersebut memberikan sebuah gaya sentripetal pada benda (bola) ?. Coba anda bayangkan ketika anda memutar bola tersebut kemudian tali yang menahan bola terputus. Maka yang terjadi adalah bola akan terpental jauh dari lintasan melingkar. Kasus kedua jika tali tersebut kendor dan tidak merengang maka otomatis bola tersebut tidak dapat bergerak melingkar. Hal ini yang membuktikan bahwa tali memberikan gaya sentripetal berupa gaya tegangan tali pada bola sehingga dapat tetap bergerak pada lintasan melingkar.

Ada 2 jenis gerak meingkar, yaitu Gerak Melingkar Beraturan (GMB) dan Gerak Melingkar Berubah Beraturan (GMBB). Gerak Melingkar Beraturan (GMB) adalah gerak sebuah benda pada lintasan meingkar dengan kecepatan susut yang tetap (konstan). Sedangkan Gerak Melingkar Berubah Beraturan (GMBB) adalah gerak sebuah benda pada lintasan melingkar dengan percepatan sudut yang konstan. Pada kesempatan kali ini gammafisblog.com akan membehas mengenai Gerak Melingkar Beraturan (GMB). Untuk Gerak Melingkar Berubah Beraturan (GMBB) akan kami bahas dilain kesempatan.

Ringkasan Materi Gerak Melingkar Beraturan (GMB)

Sebelum kita memulai membahas gerak melingkar beraturan lebih jauh. Maka penting bagi kita untuk mengetahu mengenai besaran-besaran apa saja yang berhubungan dengan gerak melingkar beraturan (GMB). Hal ini bertujuan agar kita bisa jauh lebih mudah untuk memahaminnya.

1. Kecepatan Linear dan Kecapatan Sudut

Kita tinjau sebuah partikel yang bergerak rotasi pada sebuah lintasan lingkaran dengan jari-jari lintasan adalah r. Jika partikel tersebut bergerak sejauh ∆θ selama selang waktu ∆t maka jarak yang ditempuh oleh partikel tersebut adalah

Dimana ∆s adalah jarak yang ditempuh partikel, r adalah jari-jari lintasan dan ∆θ adalah sudut yang dilalui oleh partikel dalam satuan radian.

1 Putaran = 2π Rad

Jika kita bagi persamaan diatas dengan waktu ∆t maka diperoleh

Jika kita membuat selang waktu ∆t mendekati nol maka persamaan diatas menjadi persamaan differensial (turunan)

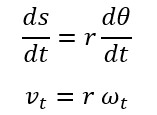
# Hubungan Vektor Kecepatan Linear dan Vektor Kecepatan Sudut

Untuk mengetahui hubungan antara Kecepatan Linear dan Kecepatan Sudut maka kita bisa meninjaunya secara vektor, karena kedua besaran ini merupakan besaran vektor yang memiliki nilai dan arah. Kemudian karena kecapatan sudut bergerak melingkar maka secara fisis benda yang bergerak secara melingkar (rotasi) maka berhubungan dengan Perkalian Silang (Cross Product) Dari Dua Vektor.

Penjelasan Sederhana Mengenai Gambar
Jika anda perhatikan gambar di atas, gambar bagian kanan merupakan ilustrasi bagaimana hubungan antara vektor kecepatan linear dan vektor kecepatan sudut. Untuk memudahkan kita memahami gambar diatas maka disini coba kita bayangkan sebuah tutup botol. Jika tutup botol kita putar ke kanan (searah jarum jam) maka botol akan tertutup, maka dari itu arah kecepatan sudut adalah kebawah. Sebaliknya jika kita memutar tutup botol ke kiri (berlawanan jarum jam) maka vektor kecepatan sudut akan ke atas dan botol akan terbuka. Anda bisa memcobanya sendiri dengan mengambil sebuah botol dan memutarkan tutup ke kiri dan kekanan.

Untuk lebih lengkapnya kita bisa menggunakan konsep vektor dalam membahas masalah ini. Anda bisa membacanya pada artikel sebelumnya melalui link diatas. Konsep vektor yang dapat menjelaskan hubungan antara vektor kecepatan sudut dan linear adalah konsep perkalian silang (Cross Product).

Karena menggunakan konsep Perkalian Silang (Cross Product) Dari Dua Vektor maka kita dapat menggunakan kaidah atau aturan tangan kanan. Dari konsep tersebut maka diperoleh hubungan antara vektor kecepatan linear dan vektor kecepatan sudut adalah

Gerak Melingkar Beraturan (GMB) adalah gerak suatu benda pada lintasan melingkar dengan kecepatan sudut yang konstal. Besarnya kecepatan sudut dapat kita peroleh dari persamaan di atas. Karena vektor kecepatan sudut tegak lurus dengan bidang lingkaran, maka kecepatan sudut tegak lurus dengan vektor jari-jari. Artinya sudut yang dibentuk adalah 90 derajat dan sin 90 = 1.

2. Percepatan Sentripetal

Gambar 1

Percepatan sentripetal adalah percepatan yang selalu tegak lurus dengan jari-jari lingkaran dan selalu mengarah ke pusat lingkaran. Untuk mendefinisikan besarnya percepatan sentripetal maka kita dapat menganalisis gerak melingkar pada gambar 1.

Untuk mendapatkan vektor percepatan sentripetal maka kita bisa perhatikan vektor kecepatan dan dan posisi pada gambar 1. Jika benda tersebut bergerak dari A ke B sejauh ∆θ maka sudut yang dibentuk oleh vektor posisi adalah ∆θ. Karena vektor posisi (r) dan vektor kecepatan (v) tegak lurus maka sudut antara vektor kecepatan (vi dan vf) juga sama dengan ∆θ. Karena sudut kedua segitiga sama dan panjang sisi-sisi segi tiga sama maka rasionya adalah sama:

Untuk menghitung besarnya percepatan benda pada lintasan melingkar maka kita bisa menggunakan definisi percepatan rata-rata:

Ungkapan diatas dapat kita ubah menjadi besarnya percepatan rata-rata selama selang waktu ∆t untuk partikel yang bergerak dari posisi A ke B.

Sekarang kita bayangkan jarak antara titik A ke B menjadi sangat dekat dan mendekati Nol, maka percepatan rata-rata akan menjadi percepatan sesaat dengan interval waktu ∆t -> 0.

Maka besarnya percepatan sentripetal adalah

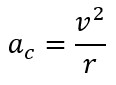
3. Gaya Sentripetal

Gaya sentripetal adalah sebuah gaya yang menyebabkan benda bergerak melingkar. Sebuah benda dapat bergerak secara melingkar dikarenakan benda tersebut memiliki percepatan yang mengarah ke pusat lingkaran atau yang disebut dengan percepatan sentripetal. Percepatan sentripetal ini disebabkan oleh gaya sentripetal.

Gambar 2

Berdasarkan Hukum 2 Newton pada benda bermasa konstan "Bearnya Percepatan yang dialami oleh sebuah benda berbanding lurus dengan besarnya gaya yang diberikan pada benda tersebut". Dari Hukum 2 Newton tersebut maka dapat kita tuliskan besarnya gaya sentripetal adalah sebagai berikut

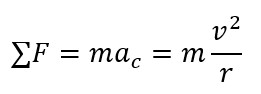
4. Kinematika Rotasi

Karena benda bergerak melingkar beraturan dan kecepatan sudut konstan, maka percepatan sudut benda tersebut akan sama dengan nol. Artinya benda tidak dipercepat ataupun diperlambat. Persamaan gerak pertikel pada lintasan melingkar memiliki bentuk yang mirip dengan persamaan gerak linear. Berikut adalah persamaan gerek partikel pada lintasan melingkar dengan kecepatan sudut konstan.

θf adalah posisi sudut akhir yang dilalui partikel
θi adalah posisi sudut awal yang dilalui partikel
ω adalah kecepatan sudut
t adalah waktu tempuh

Contoh Soal Gerak Melingkar Beraturan (GMB)

Contoh 1 : Gerak Melingkar Beraturan (GMB)

Sebuah partikel bergerak pada sebuah lintasan melingkar dengan jari-jari lingkaran adalah 100 cm. Jika partikel tersebut berputar sebanyak 2,75 putaran. Maka tentukan jarak yang ditempuh oleh partikel tersebut ?

Solusi :
Diketahui :

r = 100 cm = 1m
n = 2,75 putaran

Ditanya jarak yang ditempuh partikel (s) ?

Ingat :

s = r θ

s adalah jarak tempuh (m)
r adalah jari-jari (m)
θ posisi sudut yang dilalui partikel (radian).
1 Putaran = 2π Rad

Karena ada n putaran maka jarak yang ditempuh benda adalah

s = r nθ
s = (1 m) x (2,75) (2π)
s = 5,5π m

Jadi, jarak yang ditempu oleh partikel tersebut adalah 5,5π meter.

Contoh 2 : Gerak Melingkar Beraturan (GMB)

Diketahui bahwa sebuah benda bergerak melingkar dengan kecepatan sudut 5π rad/s. Jika jari-jari putaranya adalah 1.5 m, maka tentukan kecepan linear dari benda tersebut.

Solusi :

Diketahui

ω = 5π rad/s
r = 1.5 m

Ditanya : v ?

Jawab :

v = r ω
v = (1.5 m) ( 5π rad/s)
v =  7.5π m/s

Jadi, kecepatan linear benda tersebut adalah 7.5π m/s.

Contoh 3 : Gerak Melingkar Beraturan (GMB)

Seekor semut berada pada sebuh piringan yang berjari-jari 20 cm dan bergerak rotasi dengan kecepatan sudut 2 rad/s. Jika posisi semut adalah 10 cm dari pusat piringan maka tentukan kecepatan linear yang dialami oleh semut tersebut ?

Solusi :

Diketahui

ω = 2 rad/s
r = 10 cm = 0,1 m (Posisi semut)

Ditanya : v ?

Jawab :

v = r ω
v = (0,1 m) ( 2 rad/s)
v =  0,2 m/s

Jadi, kecepatan linear yang ditasakan oleh semut tersebut adalah 0.2 m/s.

Contoh 4 : Gerak Melingkar Beraturan (GMB)

Sebuah tali yang panjangnya 60 cm jika pada salah satu ujungnya diikatkan sebuah bola bermassa 100 gram. Kemudain ujung lainya diputar dengan kecepatan sudut tetap 5 rad/s dan bola bergerak melingkar. Maka tentukan besar gaya sentripetal yang bekerja pada sistem tersebut?

Solusi:

Diketahui:

r = 60 cm = 0,6 m

m = 100 gram = 0.1 Kg

ω = 5 rad/s

Ditanya : Gaya Sentripetal (Fs) = ...?

Jawab :

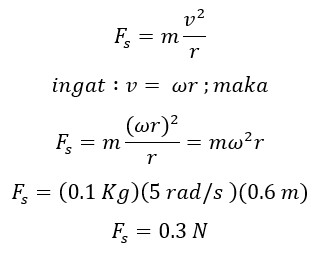
Jadi, besarnya gaya sentripetal yang membuat benda tersebut bergerak melingkar adalah 0.3 N

Baca Juga : Contoh Soal Momentum dan Hukum Kekekalan Momentum Linear

Itulah artikel tentang Ringkasan Materi Gerak Melingkar Beraturan (GMB) Beserta Contohnya. Semoga dengan artikel ini anda dapat memahami konsep gerak melingkar beraturan dan paham bagaimana cara menyelesaikan kasuk-kasus dalam gerak melingkar. Mungkin sampai di sini saja artikel kali ini. Untuk lebih lengkapnya anda bisa tanyakan melalui kolom komentar dibawah ini.

Contoh soal fisika kelas 10 soal fisika kelas 10 semester 2 soal fisika kelas 10 semester 2 dan pembahasannya latihan soal fisika kelas 10 contoh soal fisika kelas 9 soal fisika kelas 8 semester 2 Latihan soal Fisika kumpulan soal fisika kelas 10 latihan soal fisika kelas 10 semester 2 kumpulan soal fisika smp dan pembahasannya kumpulan soal fisika kelas 11 soal fisika kelas 7 semester 1 latihan soal fisika kelas 12 semester 1 download soal fisika kelas 11.

Jangan Lupa Untuk Share :-)

Share this post